Chapter 8: Queues

영화 티켓을 구매하거나 프리터가 출력물을 인쇄할 때 큐(Queue) 자료구조와 같은 방식으로 진행된다. Queue는 FIFO(first-in first-out, 선입 선출)이다. 즉, 첫 번째로 추가된 요소가 항상 가장 먼저 제거된다. Queue는 요소의 처리 순서를 유지해야 할 때 유용하다.

 

Common operations

큐(Queue) 프로토콜(protocol)을 정의한다.

public protocol Queue {
    associatedtype Element //Swift 2.2 부터 typealias가 associatedtype으로 변경되었다.
    //String, Int 등의 지정된 type이 아니라, 견본의 type을 지정한다.
    //실제로 사용할 type은 protocol이 구현될 때 지정된다.
    //https://zeddios.tistory.com/382
    
    mutating func enqueue(_ element: Element) -> Bool 
    //Queue의 뒤에 요소를 삽입한다. 작업이 성공하면 true를 반환한다.
    mutating func dequeue() -> Element? 
    //Queue의 앞에 있는 요소를 제거하고 이를 반환한다.
    
    var isEmpty: Bool { get } //Queue가 비어 있는지 확인한다.
    var peek: Element? { get } //요소를 제거하지 않고 Queue의 앞에 있는 요소를 반환한다.
}

위의 protocol은 Queue의 핵심적인 구현 사항을 설명한다.

• enqueue : Queue의 뒤에 요소를 삽입한다. 작업이 성공하면 true를 반환한다.
• dequeue : Queue의 앞에 있는 요소를 제거하고 이를 반환한다.
• isEmpty : Queue가 비어 있는지 확인한다.
• peek : 요소를 제거하지 않고 Queue의 앞에 있는 요소를 반환한다.

Queue는 앞쪽에서 요소를 제거하고, 뒷쪽에서 요소를 삽입한다. 앞쪽과 뒷쪽 사이의 요소에 대해서는 신경쓸 필요 없다. 만약 그 요소들을 알아야 한다면, Array를 사용해야 한다.

 

Example of a queue

Queue를 이해하기 가장 쉬운 방법은 현실의 예를 생각해 보는 것이다. 사람들이 영화표를 구매하기 위해 줄을 서 있는 것을 상상할 수 있다. 

Queue에는 현재 Ray, Brian, Sam, Mic이 있다. Ray가 티켓을 구매하면, 줄을 이탈한다. dequeue()를 호출하여 Queue의 앞쪽(front)에서 Ray가 제거된다. Brian이 이제 줄의 가장 앞에 있으므로, peek을 호출하면 Brian을 반환한다. Vicki가 티켓을 구매하기 위해 줄을 서면, Vicki는 enqueue("Vicki") 되어 Queue의 뒤(back)에 추가된다. 다음 4가지 방법으로 Queue를 만드는 방법을 알아 본다.

• Array
• Doubly Linked List
• Ring Buffer
• Two Stack

 

Array-based implementation

Swift standard library에는 고급 추상화(higher-level abstraction)를 구축하는데 최적화된 기본 자료구조 세트가 있다. 그 중 하나는 순서가 지정된 요소를 연속적인 list로 저장하는 자료구조인 배열(Array)이다. 여기에서는 Array를 사용해 Queue를 생성한다.

 

public struct QueueArray<T>: Queue { 
    //Queue protocol을 구현한다. Queue에서 정의한 Element는 T로 유추된다.
    private var array: [T] = []
    public init() {}
}

Generic 구조로 Queue를 정의한다. 계속해서, protocol을 준수하도록 Queue 구현을 완료해야 한다.

 

Leveraging arrays

extension QueueArray { //Queue protocol에서 정의된 메서드와 변수들을 구현해 준다.
    public var isEmpty: Bool { //Queue가 비어 있는 지 확인한다.
        array.isEmpty
    }
    
    public var peek: T? { //Queue의 가장 첫 번째 요소를 삭제하지 않고 반환한다.
        array.first
    }
}

Array의 기능을 사용하면, 위와 같은 잡업을 손쉽게 구현할 수 있다. 이 작업들의 시간 복잡도는 모두 O(1) 이다.

 

Enqueue

Array로 Queue를 구축하면, Queue의 뒤에 요소를 추가하는 것 또한 쉽게 구현할 수 있다.

extension QueueArray {
    public mutating func enqueue(_ element: T) -> Bool { 
    //Queue의 뒤에 요소를 삽입한다. Array로 구현하는 경우에는 단순히 append 해 주면 된다.
        array.append(element)
        return true
    }
}

enqueue의 시간 복잡도는 평균적으로 O(1) 이다. 보통은 Array에 빈 공간이 있기 때문이다.

위의 예제에서 Mic을 추가하면, Array에 빈 공간이 두 개 남게 된다. 여러 요소를 계속 추가하다보면, Array가 가득 차게 된다. 할당된 것보다 많은 공간을 사용하려면, 추가적인 공간을 확보해야 하므로 Array의 크기를 조정해야 한다.

이 경우에는 Array를 새 메모리에 할당하고 기존의 데이터를 복사해야 하므로 O(n) 이 소요된다. 하지만, 공간이 부족할 때마다 용량을 2배로 늘리기 때문에 이 작업은 자주 발생하지 않는다. 결과적으로 enqueue의 평균적인 비용(amortized cost, 분할 상환된 비용)은 O(1) 이 된다. 최악의 경우에는 복사를 수행해야 하므로, O(n) 이 된다.

 

Dequeue

Array로 Queue를 구축하면, 앞에서 요소를 제거하는 dequeue 작업은 enqueue에 비해 추가적인 작업이 필요하다.

extension QueueArray {
    public mutating func dequeue() -> T? {
        isEmpty ? nil : array.removeFirst() 
        //Queue가 비어 있으면 nil을 반환하고, 그렇지 않으면 array의 첫 요소를 제거한 후 반환한다.
    }
}

 

Queue의 첫 번째 요소를 제거하는 dequeue 작업의 시간 복잡도는 O(n) 이다. Queue에서 첫 요소를 제거하면, 나머지 모든 요소를 메모리에서 하나씩 앞으로 이동해야 하기 때문에 선형 시간(linear time)이 소요된다.

 

Debug and test

extension QueueArray: CustomStringConvertible {
    public var description: String {
        String(describing: array) 
        //Array에 구현된 CustomStringConvertible를 사용한다.
    }
}

구현을 확인해 본다.

var queue = QueueArray<String>()
queue.enqueue("Ray") // true
queue.enqueue("Brian") // true
queue.enqueue("Eric") // true
queue // ["Ray", "Brian", "Eric"]
queue.dequeue() // "Ray"
queue // ["Brian", "Eric"]
queue.peek //"Brian" //peek은 요소를 제거하진 않는다.

 

 

Strengths and weaknesses

Array 기반 Queue를 요약하면 다음과 같다. 선형 시간(linear time)이 걸리는 dequeue를 제외한 대부분의 연산은 상수 시간(constant time) 이다. 저장 공간 또한 선형적(linear) 이다.

연산(Operations)	평균(Average case)	최악(Worst case)
enqueue	O(1)	O(n)
dequeue	O(n)	O(n)
공간 복잡도 (Space Complexity)	O(n)	O(n)

Swift standard library의 Array를 사용하면, 매우 쉽게 Queue를 구현할 수 있다. 평균적인 작업 속도 또한 매우 빠른편이다. 하지만, Array로 구현한 Queue는 몇 가지 단점이 있다. Queue의 앞에서 요소를 제거하면(dequeue), 모든 요소가 하나씩 앞으로 이동하므로 비효율적이다. Queue가 클 경우 이는 매우 큰 단점이 된다. 또한 Array가 가득 차면 크기를 조정해야 하며, 평소에는 사용하지 않고 남아 있는 공간이 있을 수 있으므로 시간이 지날수록 메모리 사용량이 증가할 수 있다. 이런 단점을 해결하기 위해 Linked List로 Queue를 구현할 수 있다.

 

Doubly linked list implementation

이중 연결 리스트(Doubly linked list)는 이전 node에 대한 참조가 추가된 연결 리스트(Linked List) 이다.

public class QueueLinkedList<T>: Queue {
    private var list = DoublyLinkedList<T>()
    
    public init() {}
}

QueueArray와 비슷하지만, Array 대신 DoublyLinkedList를 사용한다. 다음으로 Queue protocol을 구현한다.

 

Enqueue

extension QueueLinkedList {
    public func enqueue(_ element: T) -> Bool {
        list.append(element)
        
        return true
    }
}

 

DoublyLinkedList는 tail node를 new node로 지정하고, previous와 next 참조를 업데이트 한다. 이 작업의 시간 복잡도는 O(1) 이다.

 

Dequeue

extension QueueLinkedList {
    public func dequeue() -> T? {
        guard !list.isEmpty, let element = list.first else { 
            //list가 비어 있지 않고, 첫 요소가 존재하는지 확인한다.
            return nil
        }
        
        return list.remove(element) 
        //Queue의 첫 요소를 제거하고 반환한다.
    }
}

list의 앞에서 요소를 제거하는 작업도 O(1) 이다. Array 구현과 달리, 요소를 하나씩 앞으로 이동할 필요 없다. 대신, Linked List의 처음 두 node의 참조를 업데이트 하면 된다.

 

Checking the state of a queue

Array 구현과 유사하게, DoublyLinkedList의 속성을 사용하여, peek과 isEmpty를 구현할 수 있다.

extension QueueLinkedList {
    public var peek: T? {
        list.first?.value
    }
    
    public var isEmpty: Bool {
        list.isEmpty
    }
}

 

Debug and test

디버깅을 위해, CustomStringConvertible를 추가한다.

extension QueueLinkedList: CustomStringConvertible {
    public var description: String { 
    //DoublyLinkedList에 구현된 것을 사용한다.
        String(describing: list)
    }
}

연결 리스트(Linked List)를 사용해 Queue를 구현한다.

var queue = QueueLinkedList<String>()
queue.enqueue("Ray") // true
queue.enqueue("Brian") // true
queue.enqueue("Eric") // true
queue // Ray -> Brian -> Eric -> end
queue.dequeue() // "Ray"
queue // Brian -> Eric -> end
queue.peek // "Brian"

QueueArray와 동일한 결과를 출력한다.

 

Strengths and weaknesses

DoublyLinkedList 기반 Queue를 요약하면 다음과 같다.

연산(Operations)	평균(Average case)	최악(Worst case)
enqueue	O(1)	O(1)
dequeue	O(1)	O(1)
공간 복잡도 (Space Complexity)	O(n)	O(n)

QueueArray의 중요 문제 중 하나는 요소를 dequeue할 때, 선형 시간(linear time)이 걸린다는 것이다. Linked List로 구현하면, node의 previous와 next 참조를 업데이트 하기만 하면 되므로 상수 시간(constant time)인 O(1) 으로 시간 복잡도를 줄일 수 있다. QueueLinkedList의 단점은 표에서는 확인할 수 없지만, 시간 복잡도가 O(1)임에도 불구하고 높은 오버헤드가 발생한다는 것이다. 각 요소에는 정방향과 역방향 참조를 위한 추가적인 저장공간이 있어야 한다. 또한 새 요소를 만들 때마다 상대적으로 큰 비용이 드는 동적 할당(dynamic allocation)이 필요하다. 반대로, QueueArray는 한번에 대량 할당 하므로 더 효율적이다. 할당(allocation)에 오버헤드(overhead)를 발생 시키지 않으면서, O(1) 로 dedequeue 할 수 있는 구현도 있다. 더 이상 추가 공간이 필요하지 않은 크기가 고정된 Queue의 경우에는 링 버퍼(Ring buffer)와 같은 방식을 사용해 성능을 향상 시킬 수 있다. 예를 들어, 5명이서 Monopoly 게임을 하는 경우, 링 버퍼를 기반으로 하는 Queue를 사용해, 다음 차례를 추적(track)할 수 있다.

 

Ring buffer implementation

Circular buffer이라고도 하는 Ring buffer는  고정 크기(fixed-size)의 Array이다. 이 자료구조(data structure)는 마지막에 제거할 요소가 더 이상 없을 때, 앞 부분을 연결한다. 링 버퍼를 사용해 Queue를 구현하는 간단한 예시는 다음과 같다.

크기가 4로 고정된 Ring buffer를 생성한다. Ring buffer에는 두 개의 참조가 있다.

1. read 포인터는 Queue의 앞을 추적한다.
2. write 포인터는 사용가능한 다음(next) 슬롯을 추적한다. 따라서 이미 read한 기존 요소를 override 할 수 있다.

요소(item)를 enqueue한다.

Queue에 요소를 추가할 때마다 write 포인터가 1씩 증가한다. 요소를 계속 추가한다.

write 포인터가 read 포인터보다 앞서 있게 된다. 이 상태는 Queue가 비어 있지 않다는 것을 의미한다. 여기서 2개의 요소를 dequeue하면 다음과 같다.

 

dequeue는 링 버퍼(Ring Buffer)를 읽는 것과 같다. read 포인터가 이동한다. 이제 하나의 요소를 더 enqueue하여 queue를 채운다.

write포인터가 Queue의 끝에 도달했기 때문에 다시 다시 첫 index로 이동한다. 이러한 움직임 때문에 circular buffer라고 하기도 한다. 마지막으로, 두 개의 남은 요소를 dequeue한다.

read 포인터도 시작 부분으로 줄 바꿈(wrap)된다. read와 write 포인터가 같은 index를 가리키고 있다면, Queue가 비어 있는 상태를 의미한다.

해당 클래스에 대한 자세한 구현 사항은 다음에서 확인할 수 있다.
https://github.com/raywenderlich/swift-algorithm-club/tree/master/Ring%20Buffer

QueueRingBuffer를 정의하고 구현한다.

public struct QueueRingBuffer<T>: Queue {
    private var ringBuffer: RingBuffer<T>
    
    public init(count: Int) { 
        //RingBuffer의 크기는 고정되어 있으므로 count 매개변수가 필요하다.
        ringBuffer = RingBuffer<T>(count: count)
    }
    
    public var isEmpty: Bool {
        ringBuffer.isEmpty
    }
    
    public var peek: T? {
        ringBuffer.first
    }
}

Queue protocol을 준수하기 위해, isEmpty, peek 두 개의 속성을 구현해 준다. isEmpty, peek 모두 O(1) 연산이다.

 

Enqueue

extension QueueRingBuffer {
    public mutating func enqueue(_ element: T) -> Bool {
        ringBuffer.write(element) //write 포인터가 1씩 증가한다.
        //ringBuffer는 크기가 고정되어 있으므로 요소가 성공적으로 enqueue 되었는지 여부를 반환해 줘야 한다.
    }
}

ringBuffer의 write(_:)를  호출해 구현한다. enqueue(_:)는 O(1) 연산이다.

 

Dequeue

extension QueueRingBuffer {
    public mutating func dequeue() -> T? {
        ringBuffer.read() //read 포인터가 1씩 증가한다.
        //ringBuffer가 비어 있다면 nil을 반환한다.
    }
}

ringBuffer의 read(_:)를  호출해 구현한다.

 

Debug and test

extension QueueRingBuffer: CustomStringConvertible {
    public var description: String {
        String(describing: ringBuffer) 
        //ringBuffer에 구현된 문자열 표현을 위임한다.
    }
}

Ring Buffer 기반의 Queue를 구현한다.

var queue = QueueRingBuffer<String>(count: 10)
queue.enqueue("Ray") // true
queue.enqueue("Brian") // true
queue.enqueue("Eric") // true
queue // [Ray, Brian, Eric]
queue.dequeue() // "Ray"
queue // [Brian, Eric]
queue.peek // "Brian"

이전의 QueueArray, QueueLinkedList와 동일하게 작동한다.

 

Strengths and weaknesses

Ring-Buffer 기반 Queue를 요약하면 다음과 같다.

연산(Operations)	평균(Average case)	최악(Worst case)
enqueue	O(1)	O(1)
dequeue	O(1)	O(1)
공간 복잡도 (Space Complexity)	O(n)	O(n)

ring-buffer 기반의 Queue는 enqueue, dequeue에서 QueueLinkedList와 동일한 시간 복잡도를 가진다. 유일한 차이점은 공간 복잡도이다. RingBuffer의 크기는 고정되어 있어, enqueue가 실패할 수 있다. 지금까지 simple array, doubly linked-list, ring-buffer 로 구현된 queue를 살펴 봤다. 이 외에도 two stack을 사용한 Queue가 있다. 이는 spatial locality(공간적 지역성)이 Linked List보다 훨씬 효율적이며, Ring Buffer와 달리 크기가 고정되어 있지 않다.

원문에는 공간적 지역성이 spacial locality로 되어 있는데, spatial locality 오타인 것 같음.
공간적 지역성(spacial locality) : 최근 접근한 데이터의 주변 데이터에 빠르게 접근하는 것

 

Double-stack implementation

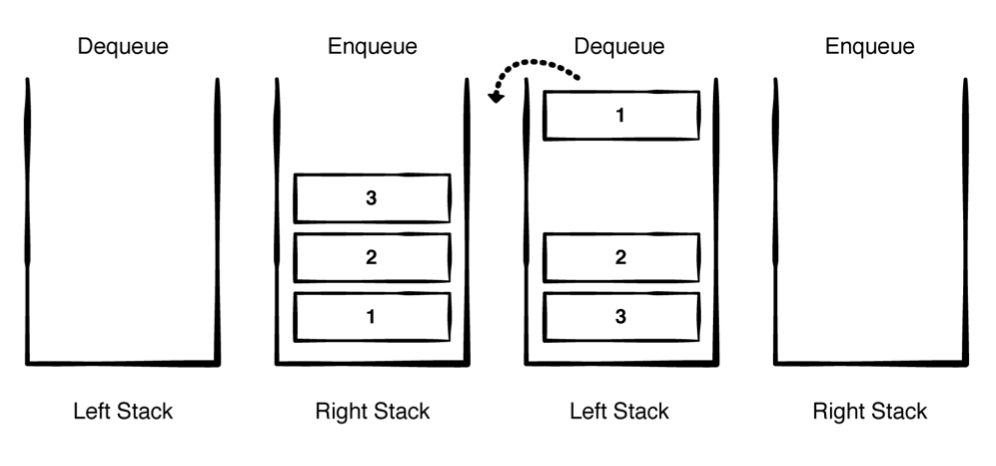
public struct QueueStack<T> : Queue {
    private var leftStack: [T] = []
    private var rightStack: [T] = []
    
    public init() {}
}

두 개의 Stack을 사용하는 아이디어는 간단하다. enqueue는 요소를 right Stack에 넣는다. 그리고, dequeue는 right Stack을 reverse하여 left Stack에 넣고 FIFO 순서대로 뺀다.

 

 

Leveraging arrays

공통적인 Queue의 기능을 구현한다.

extension QueueStack {
    public var isEmpty: Bool { //양 쪽의 Stack이 모두 비어 있는 지 확인한다.
        leftStack.isEmpty && rightStack.isEmpty
        //양쪽의 Stack이 모두 비어 있다는 의미는 dequeue할 요소가 없으며, enqueue된 요소 또한 없다는 의미이다.
    }
    
    public var peek: T? { //Stack의 맨 위 요소를 확인한다.
        !leftStack.isEmpty ? leftStack.last : rightStack.first
        //Left Stack이 비어 있지 않으면, Left Stack의 마지막(위) 요소가 Queue의 가장 앞에 있는 요소이다.
        //Left Stack이 비어 있다면, Right Stack이 reverse 되어 Left Stack에 넣어진다.
        //따라서, 이 경우에는 Right Stack의 첫(아래) 요소가 Queue의 가장 앞 요소가 된다.
    }
}

isEmpty와 peek 모두 O(1) 연산이다.

 

Enqueue

extension QueueStack {
    public mutating func enqueue(_ element: T) -> Bool {
        rightStack.append(element)
        
        return true
    }
}

Right Stack은 요소를 enqueue하는 데 사용된다. Array로 Stack을 구현하여 간단히 append 해 주면 된다. QueueArray에서의 Enqueue와 마찬가지로 O(1) 작업이다.

 

Dequeue

Double-stack에서 Dequeue를 구현하는 것은 다소 까다롭다.

extension QueueStack {
    public mutating func dequeue() -> T? {
        if leftStack.isEmpty { //leftStack이 비어 있는지 확인한다.
            leftStack = rightStack.reversed()
            //leftStack이 비어 있으면, rightStack을 reverse해 leftStack에 할당한다.
            rightStack.removeAll() 
            //rightStack의 모든 요소를 leftStack으로 옮겼으므로 삭제한다.
        }
        
        return leftStack.popLast() //leftStack의 마지막 요소를 pop한다.
    }
}

leftStack이 비어 있는 경우에만, rightStack의 요소를 옮긴다.

Array의 전체 요소를 복사하는 것은 O(n)연산이다. 하지만, 전체 dequeue의 시간 복잡도는 여전히 O(1) 로 계산한다. leftStack과 rightStack에 많은 요소가 있을 때, 모든 요소를 dequeue하려고 하면 leftStack의 모든 요소를 pop 한 뒤, rightStack을 한 번만 reverse-copy 한 다음, 계속해서 leftStack의 요소를 pop 하면 된다.

 

Debug and test

extension QueueStack: CustomStringConvertible {
    public var description: String {
        String(describing: leftStack.reversed() + rightStack)
    }
}

leftStack의 reverse와 rightStack을 결합하여 출력한다. double-stack의 구현을 확인해 본다.

 

var queue = QueueStack<String>()
queue.enqueue("Ray") // true
queue.enqueue("Brian") // true
queue.enqueue("Eric") // true
queue // ["Ray", "Brian", "Eric"]
queue.dequeue() // "Ray"
queue // ["Brian", "Eric"]
queue.peek // "Brian"

이전 모든 예시와 마찬가지로 동일하게 작동한다.

 

Strengths and weaknesses

Double-stack 기반 Queue를 요약하면 다음과 같다.

연산(Operations)	평균(Average case)	최악(Worst case)
enqueue	O(1)	O(n)
dequeue	O(1)	O(n)
공간 복잡도 (Space Complexity)	O(n)	O(n)

Array 기반 Queue와 비교해, dequeue 연산의 평균 시간 복잡도를 O(1)으로 낮출 수 있다. 또한, Double-stack 기반 Queue는 완전히 동적(dynamic)이며, ring-buffer 기반 Queue와 달리, 크기의 제한이 없다. 하지만, right stack을 reverse 하거나, 저장 공간이 부족한 최악의 경우에는 O(n)이 된다. Swift에서는 저장 공간이 부족할 때마다 매번 용량을 2배로 늘리기 때문에 이러한 경우가 자주 발생하지는 않는다. 마지막으로, 메모리 블록에서 배열의 요소가 서로 붙어 있기 때문에 spatial locality(공간적 지역성) 측면에서 Linked List를 능가한다. Double-stack Queue는 처음 액세스할 때 많은 요소가 캐시에 로드된다. 이 작업은 Array에서 O(n) 이 필요하지만, 간단한 복사 작업의 경우 메모리 대역폭에 근접한 매우 빠른 O(n) 이다.

LinkedList는 요소가 연속된 메모리 블록에 저장되지 않기 때문에, non-locality 하고, 이때문에 캐시(cash)의 누락이 생겨 액세스 시간이 늘어난다.

원문에는 공간적 지역성이 spacial locality로 되어 있는데, spatial locality 오타인 것 같음. 
공간적 지역성(spacial locality) : 최근 접근한 데이터의 주변 데이터에 빠르게 접근하는 것

 

Key points

• Queue는 FIFO 자료구조이다. 먼저 추가된 요소를 먼저 제거해야 한다.
• Enqueue는 Queue의 뒤에 요소를 삽입한다.
• Dequeue는 Queue에서 요소를 제거한다.
• Array의 요소는 인접한 메모리 블록에 배치되지만, Linked List의 요소는 분산되어 배치되므로 캐시가 누락될 가능성이 크다.
• Ring-buffer Queue는 고정된 크기의 Queue에 적합하다.
• 다른 자료 구조(Data Structure)와 비교할 때, 두 개의 Stack을 활용한 Queue의 경우 dequeue(_:)의 평균적 시간복잡도가 O(1)으로 개선된다.
• Double-stack Queue는 공간적 지역성(spatial locality) 측면에서 Linked-list Queue를 능가한다.