Chapter 12: Binary Trees

자식 노드의 수에 제한이 없는 일반 Tree(트리)와 달리, Binary Tree(이진 트리)는 각 node에 최대 두 개의 자식이 있다. 이 자식들을 각각 위치에 따라 left, right라고 부른다.

 

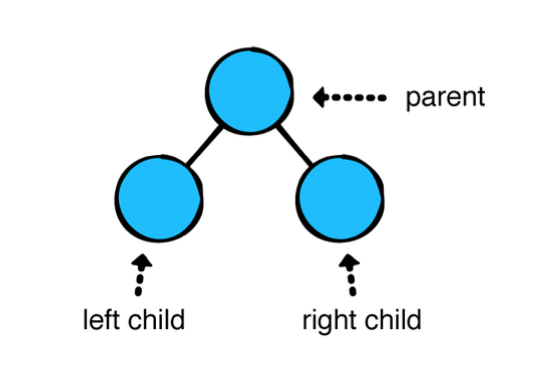
이진 트리는 많은 트리 구조 알고리즘의 기초가 된다.

 

Implementation

public class BinaryNode<Element> {
    public var value: Element
    public var leftChild: BinaryNode?
    public var rightChild: BinaryNode?
    
    public init(value: Element) {
        self.value = value
    }
}

BinaryNode를 사용해 이진트리를 구현한다.

var tree: BinaryNode<Int> = {
    let zero = BinaryNode(value: 0)
    let one = BinaryNode(value: 1)
    let five = BinaryNode(value: 5)
    let seven = BinaryNode(value: 7)
    let eight = BinaryNode(value: 8)
    let nine = BinaryNode(value: 9)
    
    seven.leftChild = one
    one.leftChild = zero
    one.rightChild = five
    seven.rightChild = nine
    nine.leftChild = eight
    
    return seven
}() //클로저

 

Building a diagram

자료구조(Dats Structure)의 다이어그램을 작성하면, 작동방식을 이해하는 데 도움이 될 수 있다. 콘솔(Console)에서 이진 트리를 시각화하는 데 도움이 되는 재사용 가능한 알고리즘을 구현한다.

이 알고리즘은 Károly Lőrentey의 책, Optimizing Collections에서 가져왔다.
https://www.objc.io/books/optimizing-collections/

extension BinaryNode: CustomStringConvertible {
    public var description: String {
        diagram(for: self)
    }
    
    private func diagram(for node: BinaryNode?,
                         _ top: String = "",
                         _ root: String = "",
                         _ bottom: String = "") -> String {
        guard let node = node else {
            return root + "nil\n"
        }
        
        if node.leftChild == nil && node.rightChild == nil {
            //자식 노드가 없는 경우(leaf)
            return root + "\(node.value)\n"
        }
        
        return diagram(for: node.rightChild, top + " ", top + "┌──", top + "│ ")
            + root + "\(node.value)\n"
            + diagram(for: node.leftChild, bottom + "│ ", bottom + "└──", bottom + " ")
    }
}

이진 트리 다이어그램(diagram)을 나타내는 문자열을 재귀적으로 생성한다. 위에서 작성한 트리로 확인해 본다.

example(of: "tree diagram") {
    print(tree)
    //  ┌──nil
    // ┌──9
    // │ └──8
    // 7
    // │ ┌──5
    // └──1
    //  └──0
}

출력은 다음과 같다.

    ┌──nil
┌──9
│ └──8
7
│ ┌──5
└──1
    └──0

해당 알고리즘은 모든 이진트리에서 사용할 수 있다.

 

Traversal algorithms

이전의 트리 순회 알고리즘과 유사한 방식으로 구현하되, 몇 가지 수정이 필요하다. in-order traversal(중위 순회), pre-order traversal(전위 순회), post-order traversal(후위 순회)이 있다.

위키백과 트리 순회
https://ko.wikipedia.org/wiki/%ED%8A%B8%EB%A6%AC_%EC%88%9C%ED%9A%8C

 

In-order traversal

In-order traversal(중위 순회)는 Root에서 시작해 다음과 같은 순서로 순회한다(LPR).

• 현재 노드에서 왼쪽 자식이 있으면, 재귀적으로 먼저 순회 한다(L).
• 이후, 기존의 노드를 방문한다(P, 가운데, parent).
• 현재 노드에서 오른쪽 자식이 있으면, 재귀적으로 순회한다(R).

위의 트리에서 중위 순회는 다음과 같다.

트리가 특정 방식으로 구조화되면(이진 탐색 트리(binary search tree )이면), 중위순회는 오름차순으로 출력된다.

extension BinaryNode {
    public func traverseInOrder(visit: (Element) -> Void) {
        leftChild?.traverseInOrder(visit: visit)
        visit(value)
        rightChild?.traverseInOrder(visit: visit)
        //위의 규칙대로(LPR) 순회를 구현하면 된다.
    }
}

가운데 value를 방문하기 전에 왼쪽 node를 먼저 방문 한다. 그런 다음, 중간을 거쳐 오른쪽 node로 이동하면서 순회하면 된다. 재귀적으로 호출되므로, leftChild의 leftChild, leftChild, ... 최하단의 좌측 leaf 까지 가게 된 후, visit(value)가 호출된다.

example(of: "in-order traversal") {
    tree.traverseInOrder { print($0) }
    // 0
    // 1
    // 5
    // 7
    // 8
    // 9
}

출력은 다음과 같다.

---Example of in-order traversal---
0
1
5
7
8
9

 

Pre-order traversal

Pre-order traversal(전위 순회)는 현재 노드를 먼저 방문한 다음 왼쪽 및 오른쪽 하위 노드를 재귀적으로 방문한다(PLR).

extension BinaryNode {
    public func traversePreOrder(visit: (Element) -> Void) {
        visit(value)
        leftChild?.traverseInOrder(visit: visit)
        rightChild?.traverseInOrder(visit: visit)
        //PLR
    }
}

구현을 확인해 본다.

example(of: "pre-order traversal") {
    tree.traversePreOrder { print($0) }
    // 7
    // 0
    // 1
    // 5
    // 8
    // 9
}

출력은 다음과 같다.

---Example of pre-order traversal---
7
1
0
5
9
8

 

Post-order traversal

Post-order traversal(후위 순회)는 왼쪽 및 오른쪽 노드를 재귀적으로 방문한 후, 현재 노드를 방문한다(LRP).

즉, 해당 노드는 자신을 방문하기 전에 자식 노드를 먼저 순회한다. 따라서 Root 노드를 항상 마지막에 방문한다.

extension BinaryNode {
    public func traversePostOrder(visit: (Element) -> Void) {
        leftChild?.traverseInOrder(visit: visit)
        rightChild?.traverseInOrder(visit: visit)
        visit(value)
        //LRP
    }
}

구현을 확인해 본다.

example(of: "post-order traversal") {
    tree.traversePostOrder { print($0) }
    // 0
    // 5
    // 1
    // 8
    // 9
    // 7
}

출력은 다음과 같다.

---Example of post-order traversal---
0
5
1
8
9
7

이러한 순회 알고리즘은 각각 시간과 공간 복잡도가 모두 O(n) 이다. 이진 탐색 트리(Binary Search Tree)를 중위 순회하면 오름차순으로 출력할 수 있다.

 

Key points

• 이진 트리(binary tree)는 가장 중요한 트리 구조의 기초가 된다. 이진 검색 트리(Binary search tree)와 AVL 트리(AVL tree)는 삽입과 삭제에 제한을 주는 이진트리이다.
• in-order traversal(중위 순회), pre-order traversal(전위 순회), post-order traversal(후위 순회)는 이진 트리에서만 중요한 것이 아니다. 어떤 트리에서든 데이터를 처리한다면, 순회를 자주 사용하게 된다.