Chapter 41: Depth-First Search Challenges

Challenge 1: BFS or DFS

다음 두 예에서, 두 노드(node) 사이에 경로(path)가 존재하는지 여부를 확인하는데 어떤 순회 방법(BFS, DFS)이 더 나은지 생각해 본다.

 

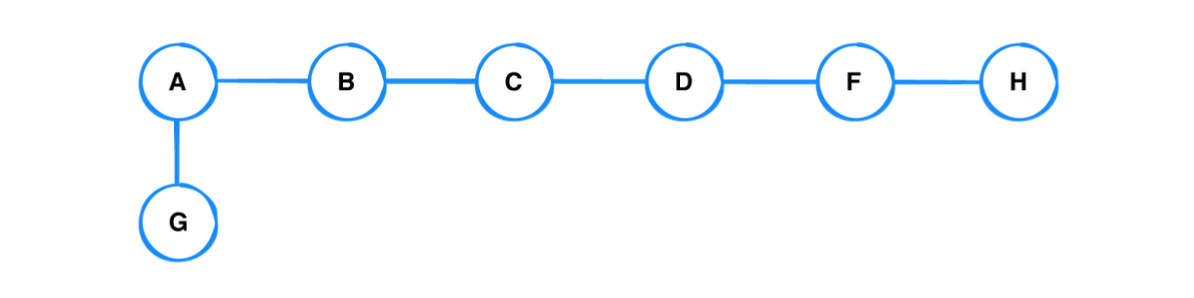
• A에서 F로 가는 경로(path)
• A에서 G로 가는 경로(path)

 

Solution

• A에서 F로 가는 경로(path) : 찾고자 하는 경로가 그래프(Graph)에서 깊기 때문에 DFS(depth-first search)를 사용하는 것이 좋다.
• A에서 G로 가는 경로(path) : 찾고자 하는 경로가 Root에 가까이 있으므로, BFS(breadth-first search)를 사용하는 것이 좋다.

---

Challenge 2: Recursive DFS

이전에는 DFS를 반복적(iterative)으로 구현 했다. 재귀(recursive)로도 DFS를 구현할 수 있다.

 

Solution

extension Graph where Element: Hashable {
    func depthFirstSearch(from source: Vertex<Element>) -> [Vertex<Element>] {
        var visited: [Vertex<Element>] = [] //방문한 정점을 순서대로 추적한다.
        var pushed: Set<Vertex<Element>> = [] //어떤 정점을 방문했는지 추적한다.
        depthFirstSearch(from: source, visited: &visited, pushed: &pushed)
        //helper 함수를 호출하여, DFS를 재귀적으로 수행한다.
        
        return visited
    }
}

helper 함수(function)은 다음과 같다.

extension Graph where Element: Hashable {
    func depthFirstSearch(from source: Vertex<Element>, visited: inout [Vertex<Element>], pushed: inout Set<Vertex<Element>>) {
        pushed.insert(source) //source 정점을 방문한 것으로 표시한다.
        visited.append(source)
        
        let neighbors = edges(from: source) //해당 정점의 모든 간선을 가져온다.
        for edge in neighbors { //해당 정점의 모든 간선을 반복
            if !pushed.contains(edge.destination) { //해당 인접 정점을 아직 방문하지 않은 경우,
                depthFirstSearch(from: edge.destination, visited: &visited, pushed: &pushed)
                //재귀적으로 DFS를 수행한다.
            }
        }
    }
}

DFS의 전체 시간 복잡도(time complexity)는 O(V + E)이다.

예제로 구현을 확인해 본다.

 

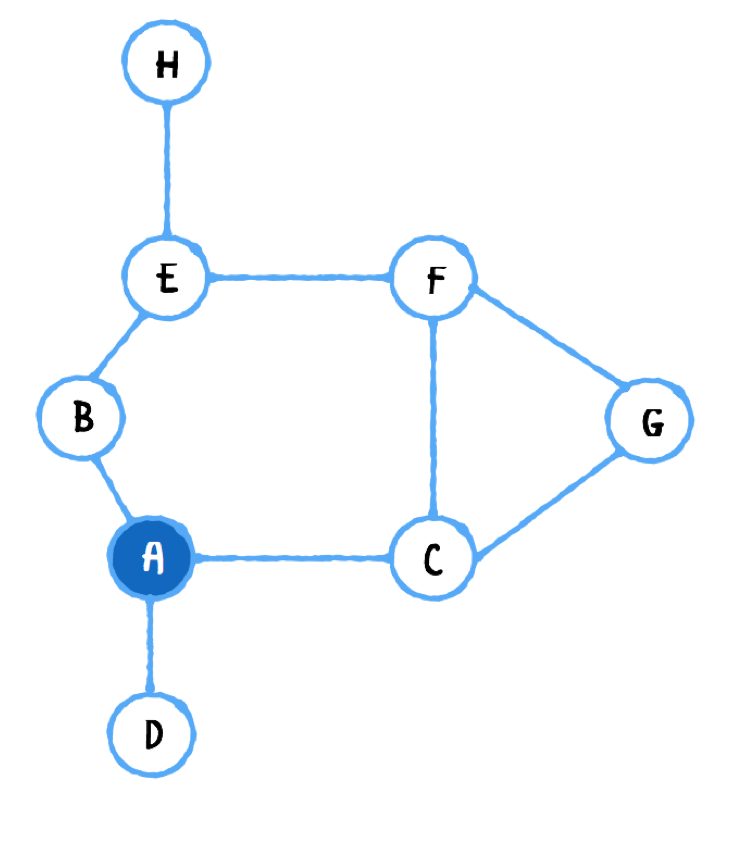
let graph = AdjacencyList<String>()
let a = graph.createVertex(data: "A")
let b = graph.createVertex(data: "B")
let c = graph.createVertex(data: "C")
let d = graph.createVertex(data: "D")
let e = graph.createVertex(data: "E")
let f = graph.createVertex(data: "F")
let g = graph.createVertex(data: "G")
let h = graph.createVertex(data: "H")

graph.add(.undirected, from: a, to: b, weight: nil)
graph.add(.undirected, from: a, to: c, weight: nil)
graph.add(.undirected, from: a, to: d, weight: nil)
graph.add(.undirected, from: b, to: e, weight: nil)
graph.add(.undirected, from: c, to: g, weight: nil)
graph.add(.undirected, from: e, to: f, weight: nil)
graph.add(.undirected, from: e, to: h, weight: nil)
graph.add(.undirected, from: f, to: g, weight: nil)
graph.add(.undirected, from: f, to: c, weight: nil)

print(graph)
// 0: A ---> [ 1: B, 2: C, 3: D ]
// 1: B ---> [ 0: A, 4: E ]
// 2: C ---> [ 0: A, 5: F, 6: G ]
// 3: D ---> [ 0: A ]
// 4: E ---> [ 1: B, 7: H, 5: F ]
// 5: F ---> [ 2: C, 4: E, 6: G ]
// 6: G ---> [ 2: C, 5: F ]
// 7: H ---> [ 4: E ]

DFS를 확인한다.

let vertices = graph.depthFirstSearch(from: a)
vertices.forEach { vertex in
  print(vertex)
    // 0: A
    // 1: B
    // 4: E
    // 5: F
    // 6: G
    // 2: C
    // 7: H
    // 3: D
}

---

Challenge 3: Detect a cycle

방향 그래프(directed graph)에서 사이클(cycle)을 감지하는 메서드(method)를 그래프(Graph)에 추가한다.

 

Solution

그래프(graph)에서 동일한 source로 이어지는 간선(edges)과 정점(vertices)의 경로(path)가 있는 경우, 이를 사이클(cycle)이라 한다. 특정 정점에서 출발하여 다시 처음 출발했던 정점으로 되돌아 올 수 있다면 사이클(cycle)이 있다고 한다.

extension Graph where Element: Hashable {
    func hasCycle(from source: Vertex<Element>) -> Bool  {
        var pushed: Set<Vertex<Element>> = [] //방문한 모든 정점을 추적하는 데 사용한다.
        
        return hasCycle(from: source, pushed: &pushed) 
        //helper 메서드를 호출하여, 그래프에 cycle이 있는지 재귀적으로 확인한다.
    }
}

helper 함수(function)은 다음과 같다.

extension Graph where Element: Hashable {
    func hasCycle(from source: Vertex<Element>, pushed: inout Set<Vertex<Element>>) -> Bool {
        pushed.insert(source) //source 정점을 insert 하면서 알고리즘을 시작한다.
        
        let neighbors = edges(from: source) //해당 정점의 모든 간선을 가져온다.
        for edge in neighbors {
            if !pushed.contains(edge.destination) && hasCycle(from: edge.destination, pushed: &pushed) {
                //방문하지 않은 인접한 정점이 있는 경우, 해당 경로를 더 깊이 재귀적으로 탐색한다.
                return true
            } else if pushed.contains(edge.destination) { //인접 정점을 방문한 적이 있다면, cycle이 존재하는 것이다.
                return true
            }
        }
        pushed.remove(source) //잠재적인 cycle이 있는 다른 경로를 계속 찾을 수 있도록 source 정점을 제거한다.
        
        return false //cycle이 발견되지 않은 경우
    }
}

기본적으로 DFS를 사용한다. 사이클(cycle)을 찾을 때까지 한 경로(path)를 재귀적으로(recursively) 탐색하고, 다른 경로(path)를 찾기 위해 스택(stack)에서 pop 해서 역추적(back-tracking)한다. 시간 복잡도(time complexity)는 O(V + E)가 된다.

예제로 구현을 확인해 본다.

 

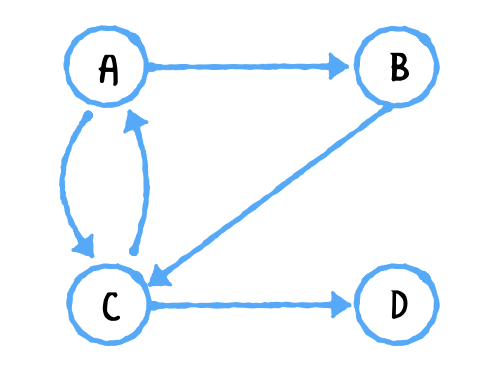
let graph = AdjacencyList<String>()
let a = graph.createVertex(data: "A")
let b = graph.createVertex(data: "B")
let c = graph.createVertex(data: "C")
let d = graph.createVertex(data: "D")

graph.add(.directed, from: a, to: b, weight: nil)
graph.add(.directed, from: a, to: c, weight: nil)
graph.add(.directed, from: c, to: a, weight: nil)
graph.add(.directed, from: b, to: c, weight: nil)
graph.add(.directed, from: c, to: d, weight: nil)

print(graph)
// 0: A ---> [ 1: B, 2: C ]
// 1: B ---> [ 2: C ]
// 2: C ---> [ 0: A, 3: D ]
// 3: D ---> [  ]

사이클(cycle)이 있는지 확인해 본다.

print(graph.hasCycle(from: a)) // true